[Algorithm] 퀵 정렬(Quick Sort)

정의

분할 정복(Divide and Conquer)법을 사용하여 정렬하는 대표적인 알고리즘

분할정복(Divice and Conquer) : 문제를 작은 2개의 문제로 분리하고 각각 해결한 다음 결과를 모아서 다시 원래의 문제를 해결하는 방법으로 대게 순환호출을 이용하여 구현한다

과정(오름차순)

1. 배열내에서 하나의 원소(피벗)을 선택한다
2. 피벗 앞쪽에는 피벗보다 작은값이, 뒤쪽에는 큰값이 오도록 피벗을 기준으로 배열을 둘로 분할한다
3. 분할된 배열을 대상으로 분할이 불가능할 때까지 위 과정을 반복한다

Python 코드(오름차순)

Not In-Place

def quick_sort(array):
    n = len(array)
    if n <= 1:
        return array
    pivot = array[n//2]
    a, b, c = [], [], []
    for num in array:
        if num < pivot:
            a.append(num)
        elif pivot < num:
            c.append(num)
        else:
            b.append(num)
    return quick_sort(a) + b + quick_sort(c)

    return array

print(quick_sort([10,1,5,8,7,6,4,3,2,9]))

In-Place

def quick_sort(arr, start, end):
    if start >= end:
        return
    key = start
    i = start+1
    j = end

    while i <= j:
        while i <= end and arr[i] <= arr[key]:
            i += 1
        while j > start and arr[j] >= arr[key]:
            j -= 1
        if i > j:
            temp = arr[j]
            arr[j] = arr[key]
            arr[key] = temp
        else:
            temp = arr[i]
            arr[i] = arr[j]
            arr[j] = temp

    quick_sort(arr, start, j-1)
    quick_sort(arr, j+1, end)

    return arr

print(quick_sort([1,10,5,8,7,6,4,3,2,9], 0, 9))

GIF로 이해하기

시간복잡도

최선 : O(N*log₂N)

• 순환 호출의 횟수 : log₂N
  레코드의 개수 N이 2의 거듭제곱이라고 가정했을 때, n=2^3일 경우 2^3 > 2^2 > 2^1 > 2^0 로 줄어들어 순환 호출깊이가 3이 된다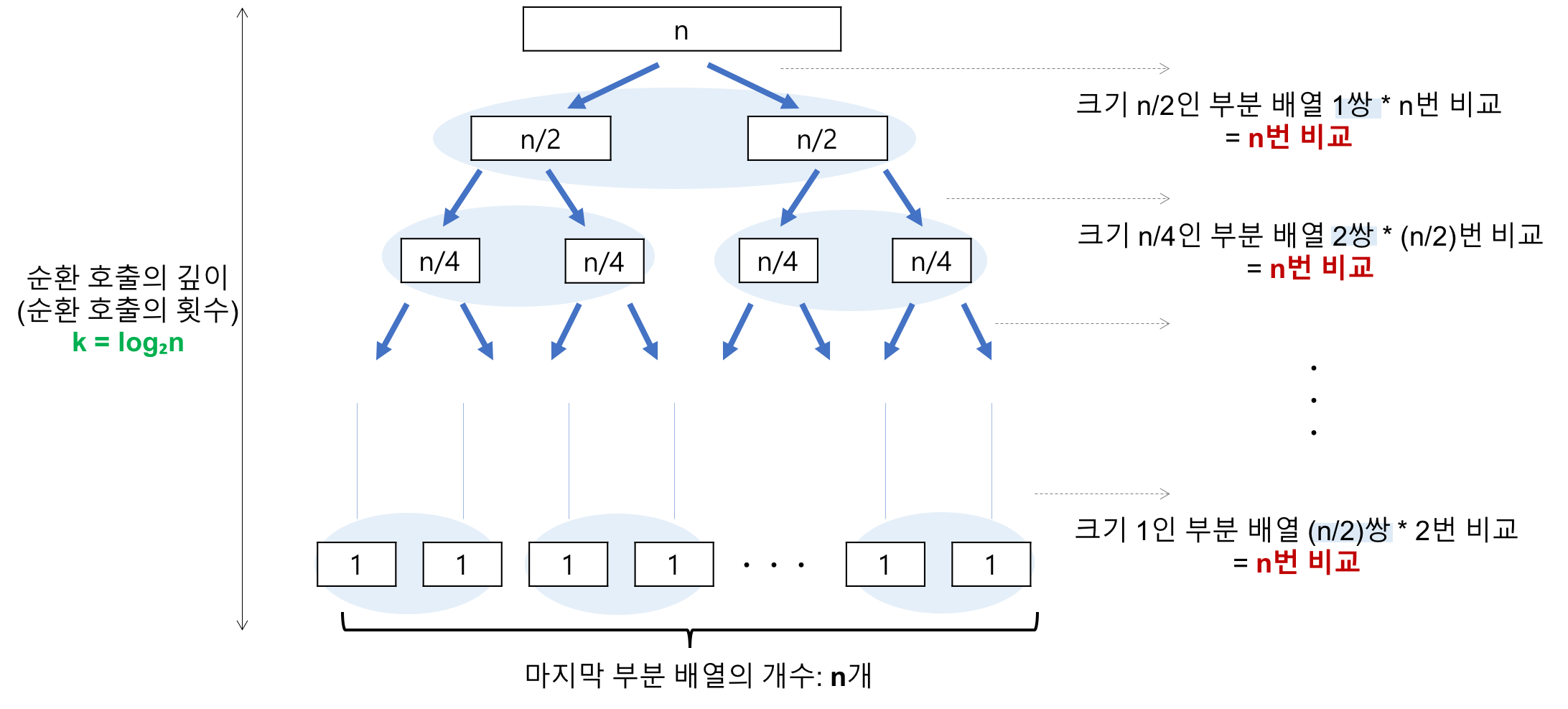

  

• 각 순환 호출 단계에서의 비교 연산 : N

• 배열이 분할되어도 평균N번 정도의 비교가 이루어진다

평균 : O(N*log₂N)

최악 : O(N^2) -> 배열이 오름차순 or 내림차순으로 정렬되어 있는 경우(불균형 분할)

• 순활 호출의 횟수 : N

  

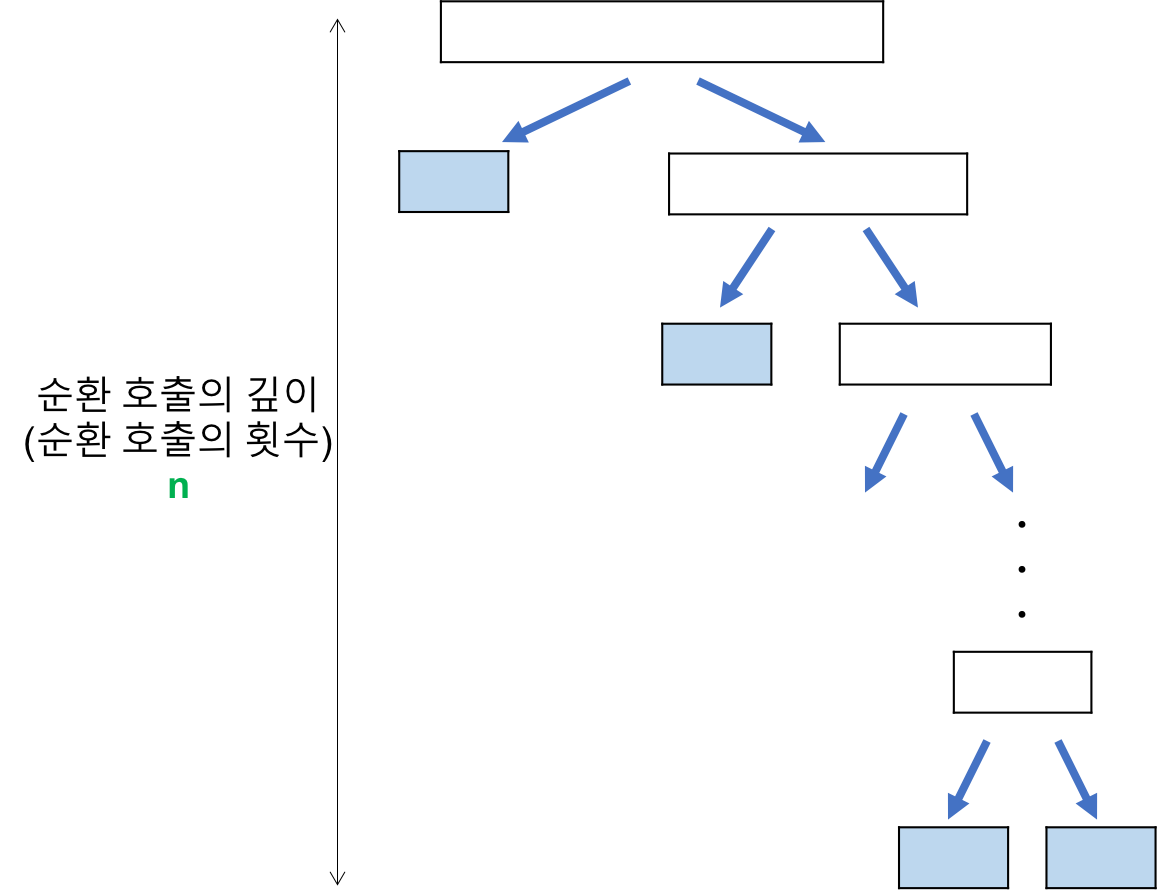
• 각 순환 호출 단계에서의 비교 연산 : N
  배열이 분할되어도 평균N번 정도의 비교가 이루어진다

특징

• 피벗값을 랜덤하게 선택하거나 중간값을 선택함으로써 평균적인 수행시간을 줄일 수 있다
• 대부분 언어의 Sort라이브러리가 퀵정렬로 구현되어 있다
• 분할 - 정복 - 결합 과정을 거친다

장점

• 평균정으로 속도가 굉장히 빠르다
• 선택정렬(Selection Sort), 버블정렬(Bubble Sort), 삽입정렬(Insertion Sort)과 마찬가지로 정렬하고자 하는 배열내에서 모든 작업이 이루어진다
  -> 제자리 정렬(In-Place_Sorting)

단점

• 시간복잡도가 피벗값의 영향을 많이 받는다
• 정렬된 데이터에 대해서는 불균형적인 분할에 의해 오히려 수행시간이 더 많이 걸린다
• 선택정렬(Selection Sort)과 마찬가지로 중복된 원소에 대하여 순서를 유지하지 않는 불안정 정렬(Unstable Sort) 이다